1 octobre 2025
Figure 1 : Système d’irrigation goutte à goutte pour le transport de l’eau et des nutriments dans le sol
L’eau, les nutriments et les défis de l’agriculture durable
L’eau et les nutriments sont des ressources essentielles à l’agriculture. Chaque saison, les agriculteurs misent sur les précipitations et l’irrigation pour s’approvisionner en eau, et sur les engrais pour fournir les nutriments essentiels comme le nitrate, le phosphore et le potassium. Or, l’eau et les nutriments ne restent pas là où ils sont appliqués : l’eau s’infiltre dans les couches du sol et les nutriments se dissolvent et se déplacent avec elle. Si ces éléments s’enfoncent trop profondément, les plantes ne peuvent plus y accéder et la nappe phréatique peut être menacée par la pollution, en particulier par les nitrates. Une gestion efficace de l’irrigation et de la fertilisation est donc vitale pour une agriculture durable et la protection de l’environnement.
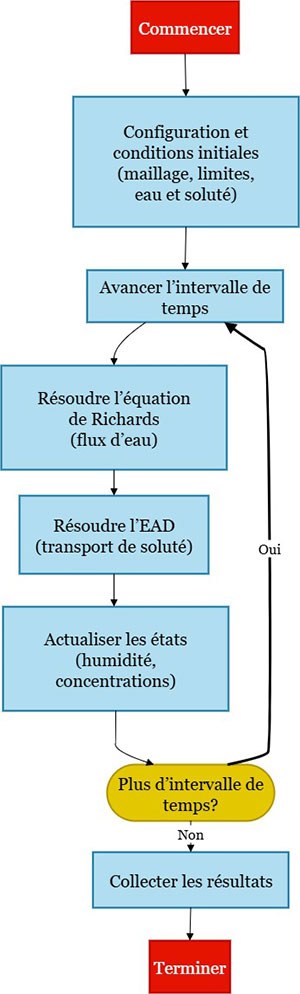
Aussi, les scientifiques recourent à des modèles mathématiques qui décrivent le mouvement de l’eau et des solutés dans les sols non saturés. Ces modèles sont un excellent moyen de prédire les résultats avant de procéder à des essais sur le terrain. Cependant, les stratégies de simulation typiques nécessitent souvent de longs calculs, freinant l’étude de scénarios multiples ou l’adaptation rapide à de nouvelles conditions. Nos travaux portent sur une approche plus rapide et plus efficace, applicable à ces simulations.
Équations fondamentales pour modéliser la dynamique de l’eau et des nutriments dans le sol
Nos travaux s’appuient sur deux équations fondamentales qui décrivent la dynamique de l’eau et des solutés dans le sol :
Équation de Richards (écoulement de l’eau) :
C(Ψ) ∂Ψ/∂t = ∇·[K(Ψ) ∇(Ψ + z)] + s(Ψ)
où Ψ est la hauteur de pression, C(Ψ) la capacité spécifique d’humidité, K(Ψ) la conductivité hydraulique non saturée, z la coordonnée verticale, et s(Ψ) un terme de puits ou source. Cette équation décrit le mouvement de l’eau dans les pores du sol, sous l’effet combiné de la gravité et des forces capillaires. Elle inclut la quantité d’eau que le sol peut retenir et la façon dont les racines absorbent l’eau.
Equation d’advection-dispersion (EAD) (transport des solutés) :
∂(θc)/∂t − ∇·(θD ∇c − c q) = 0
où θ est la teneur en eau, c la concentration en soluté, D le tenseur de dispersion, et q le flux d’eau. Cette équation décrit comment les nutriments dissous (nitrate) sont transportés par le flux d’eau (advection) et se répandent dans le sol par hétérogénéité naturelle (dispersion). Elle sert à prédire si les engrais restent dans la zone racinaire ou s’ils sont perdus plus profondément dans le sol.
Ensemble, ces équations forment un système couplé qui régit l’infiltration et le transport des nutriments dans les milieux poreux non saturés. Contrairement aux stratégies classiques, qui nécessitent souvent des calculs considérables, notre schéma numérique simule ces processus couplés de manière plus efficace tout en conservant leur précision. Cette approche nous permet d’étudier des scénarios réalistes comme les sols hétérogènes, le transport de la salinité et la fertigation (c’est-à-dire, l’apport d’engrais via l’irrigation) au nitrate sous irrigation.
Figure 2 : Diagramme de la méthodologie.
Validation du modèle et applications à la fertigation
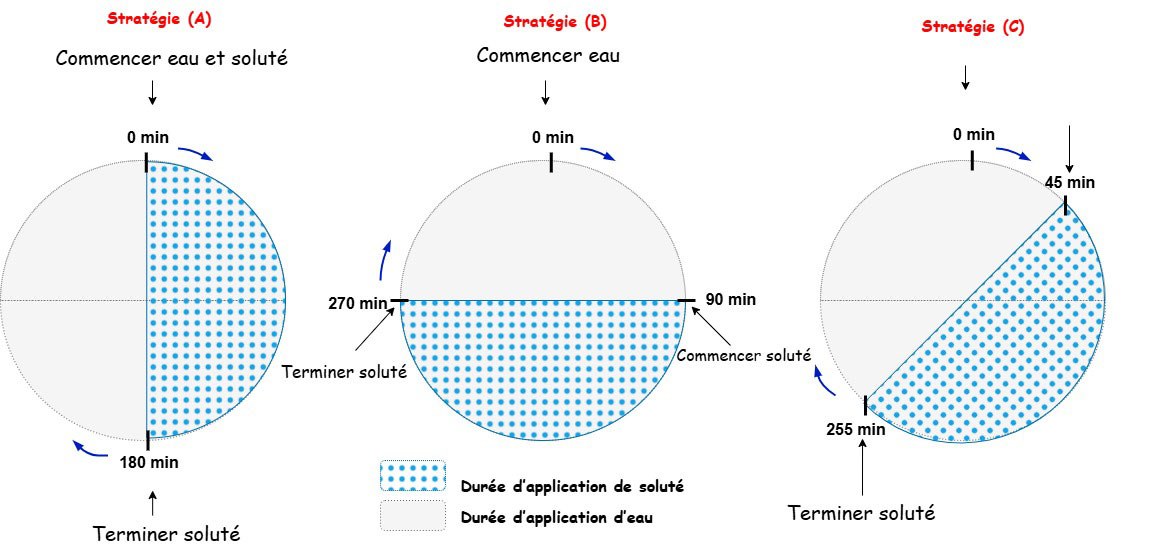
Pour valider notre méthode, nous l’avons appliquée à une série de cas tests tirés à la fois de bases de références et de données expérimentales (voir l’article original Toutlini et al. 2025a). L’une des applications les plus pratiques que nous avons testées est le transport d’engrais azoté par fertigation goutte à goutte. Cette étude de cas, réalisée par Li et al. (2005), compare trois stratégies où l’engrais est injecté à différents moments pendant l’irrigation, comme le montre la figure 3. Partant de notre nouveau schéma, nous avons simulé le même dispositif expérimental. Nos résultats correspondent étroitement aux données de laboratoire sur les profils d’humidité du sol et de concentration en nitrates.
Cette validation est importante pour deux raisons :
- Elle montre que notre schéma est non seulement plus rapide, mais aussi cohérent avec les données expérimentales.
- Elle prouve que les techniques numériques avancées peuvent résoudre des problèmes agricoles concrets comme la gestion des nitrates par l’irrigation goutte à goutte.
Figure 3 : Représentations visuelles des stratégies de fertigation. La durée totale d’irrigation est de 360 minutes (Toutlini et al. 2025a). 2025a).
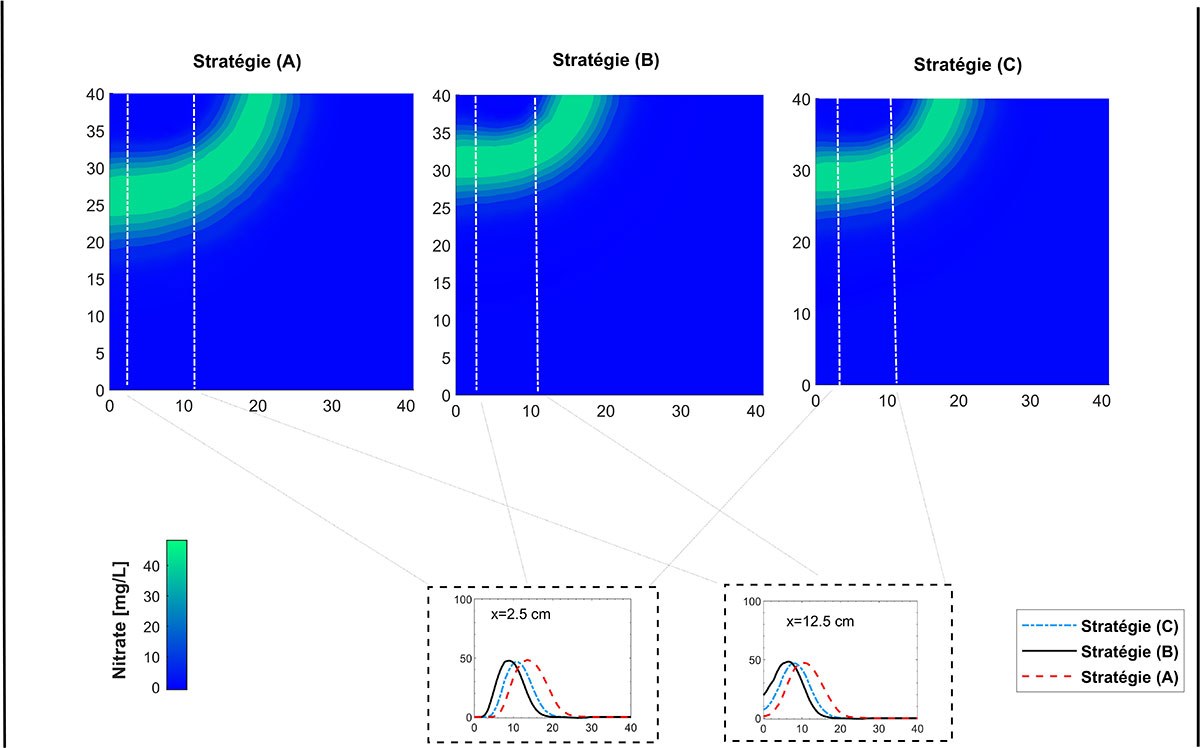
La figure 4 illustre la répartition des nitrates dans le sol après six heures de fertigation pour les trois stratégies étudiées. On y observe l’évolution spatiale des concentrations de nutriments dans la zone racinaire et en profondeur. D'après la figure 4, la stratégie B donne de bons résultats en maintenant plus longtemps les concentrations de nutriments dans la zone racinaire. Elle favorise ainsi une absorption efficace par les plantes. En revanche, les stratégies A et C entraînent un lessivage excessif des nitrates dans les couches plus profondes du sol, ce qui réduit l’efficacité des engrais et présente des risques de contamination des eaux souterraines. À noter que notre schéma a pu reproduire fidèlement ces résultats, confirmant ainsi sa capacité à reproduire des scénarios de fertigation complexes tout en réduisant considérablement les coûts de calcul. Notre approche préconise donc la conception de stratégies d’irrigation qui optimisent à la fois les rendements agricoles et la protection de l’environnement.
Figure 4 : Répartition des nitrates après 6 heures de fertigation, pour les trois stratégies, avec la méthode proposée (Toutlini et al. 2025a).
Au-delà du transport des nitrates, nos tests (dans l’article) ont montré que le schéma fonctionne bien dans d’autres cas difficiles :
- Infiltration dans des sols hétérogènes - maintient la stabilité dans des conditions difficiles.
- Recharge des nappes phréatiques - reproduit avec précision la dynamique de montée et de recharge des nappes phréatiques en conditions d’infiltration transitoires.
- Transport de la salinité des sols - reproduit les résultats de référence en moins de temps.
Conclusion
Nos recherches montrent que la modélisation mathématique avancée peut être accessible et efficace grâce aux techniques de calcul modernes. En accélérant les simulations d’absorption d’eau et de nutriments dans les sols, nous permettons aux agriculteurs, ingénieurs et scientifiques d’évaluer plusieurs stratégies d’irrigation et de fertilisation avant de les appliquer sur le terrain. Il en résulte une utilisation plus efficace des engrais, une diminution des risques environnementaux et une amélioration des rendements agricoles.
Ces travaux nous ont permis d’aller plus loin. Nous avons pu inclure plusieurs engrais comme l’urée, l’ammonium, le nitrate, le phosphore et le potassium, ainsi que les processus d’absorption d’eau et de nutriments par les racines (Toutlini et al. 2025b, c). Ces développements renforcent le potentiel du modèle à relever les défis de l’agriculture durable dans des conditions pédologiques et climatiques variées.
Références
Toutlini, N.-E., Beljadid, A., & Soulaïmani, A. (2025a). A semi-implicit second-order temporal scheme for solving the pressure head-based form of Richards' and advection–dispersion equations. Computers and Mathematics with Applications, 187, 106–131. https://doi.org/10.1016/j.camwa.2025.03.011
Toutlini, N.-E., Beljadid, A., & Soulaïmani, A. (2025b). A semi-implicit finite element method for modeling fertilizer transport through soils with root water and nutrient uptake. Mathematics and Computers in Simulation. Under Review.
Toutlini, N.-E., Soulaïmani, A., & Beljadid, A. (2025c). JAX-WSPM: A GPU-accelerated parallel framework using the JAX library for modeling water flow and solute transport in unsaturated porous media using an implicit finite element method. Computer Physics Communications, 318, 109866https://doi.org/10.1016/j.cpc.2025.109866.
Li, J., Zhang, J., & Rao, M. (2005). Modeling of water flow and nitrate transport under surface drip fertigation. Trans. ASAE, 48(2), 627-637.
