1 October 2025
Figure 1: Drip irrigation system for water and nutrient transport in soil
Water, Nutrients, and the Challenges of Sustainable Agriculture
Water and nutrients are essential resources for agriculture. Every season, farmers rely on rainfall and irrigation to supply water, while fertilizers provide key nutrients such as nitrate, phosphorus and potassium. The challenge is that water and nutrients do not remain where they are applied: water infiltrates the soil layers, and nutrients dissolve and move with it. If these elements sink too deep, plants cannot access them, and groundwater quality may be threatened by pollution, especially from nitrates. This makes efficient management of irrigation and fertilization crucial for sustainable agriculture and environmental protection.
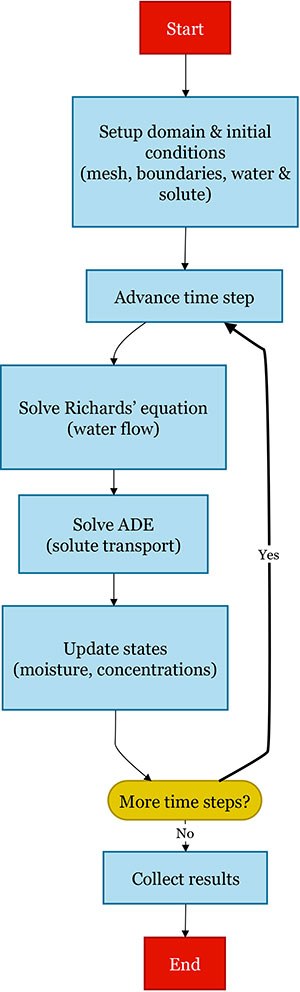
To address this, scientists use mathematical models that describe how water and solutes move in unsaturated soils. These models provide a powerful way to predict outcomes before conducting field tests. However, traditional simulation strategies often require long computation times, making it difficult to explore multiple scenarios or adapt rapidly to new conditions. Our work focuses on designing a faster and more efficient approach to these simulations.
Fundamental Equations for Modeling Water and Nutrient Dynamics in Soil
Our work is based on two fundamental equations that describe the dynamics of water and solutes in soil:
Richards equation (water flow):
C(Ψ) ∂Ψ/∂t = ∇·[K(Ψ) ∇(Ψ + z)] + s(Ψ)
where Ψ is the pressure head, C(Ψ) is the specific moisture capacity, K(Ψ) the unsaturated hydraulic conductivity, z the vertical coordinate, and s(Ψ) a sink or source term. This equation describes how water moves through soil pores under the combined effects of gravity and capillary forces. It also takes into account the amount of water the soil can hold and how roots absorb water.
Advection–dispersion equation (transport of solutes):
∂(θc)/∂t − ∇·(θD ∇c − c q) = 0
where θ is the water content, c the solute concentration, D the dispersion tensor, and q the water flux. This equation explains how dissolved nutrients such as nitrate are transported by water flow (advection) and spread through the soil due to natural heterogeneity (dispersion). It is key to predicting whether fertilizers remain in the root zone or are lost deeper into the soil.
Together, these equations form a coupled system that governs infiltration and nutrient transport in unsaturated porous media. Unlike traditional strategies, which often require heavy computation, we developed a new numerical scheme that simulates these coupled processes more efficiently while maintaining accuracy. This approach enables us to study realistic scenarios such as heterogeneous soils, salinity transport, and nitrate fertigation under irrigation.
Figure 2: Flowchart of the methodology.
Model Validation and Applications to Fertigation
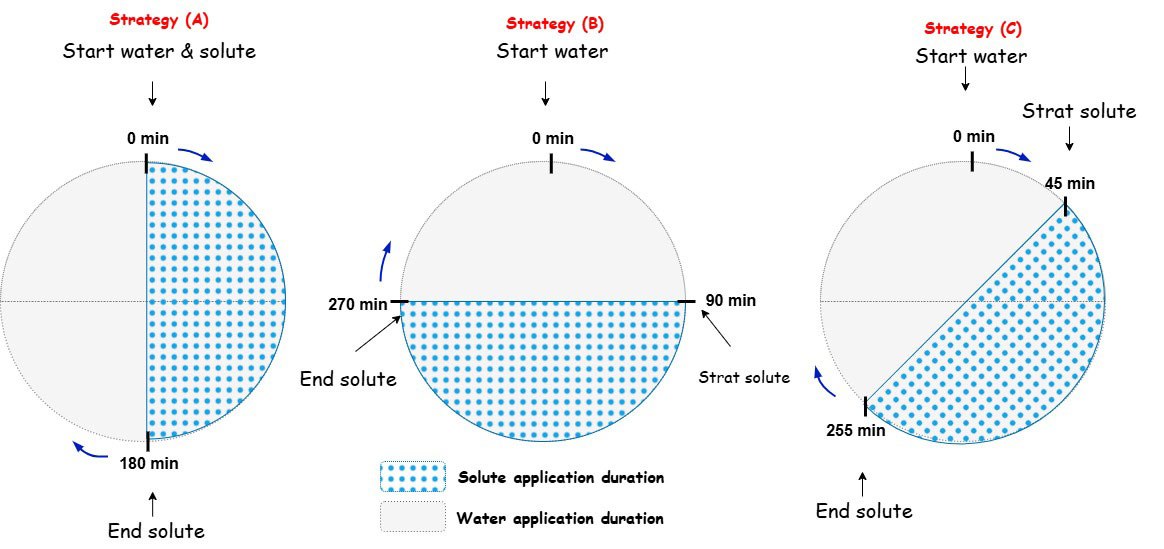
To validate our method, we applied it to a series of test cases drawn from both reference benchmarks and experimental data (see the original paper Toutlini et al. 2025a). One of the most practical applications we tested was nitrate fertilizer transport under drip fertigation. This case study, originally conducted by Li et al. (2005), compares three strategies in which fertilizer is injected at different times during irrigation, as shown in Figure 3. Using our new scheme, we simulated the same experimental setup. Our results matched the laboratory data with high precision for both soil moisture and nitrate concentration profiles.
This validation is important for two reasons:
- It shows that our scheme is not only faster, but also trustworthy when confronted with real-world experimental data.
- It proves that advanced numerical techniques can handle practical agricultural problems such as nitrate management under drip irrigation.
Figure 3: Visual representations of fertigation strategies. The total irrigation time is 360 min (Toutlini et al. 2025a).
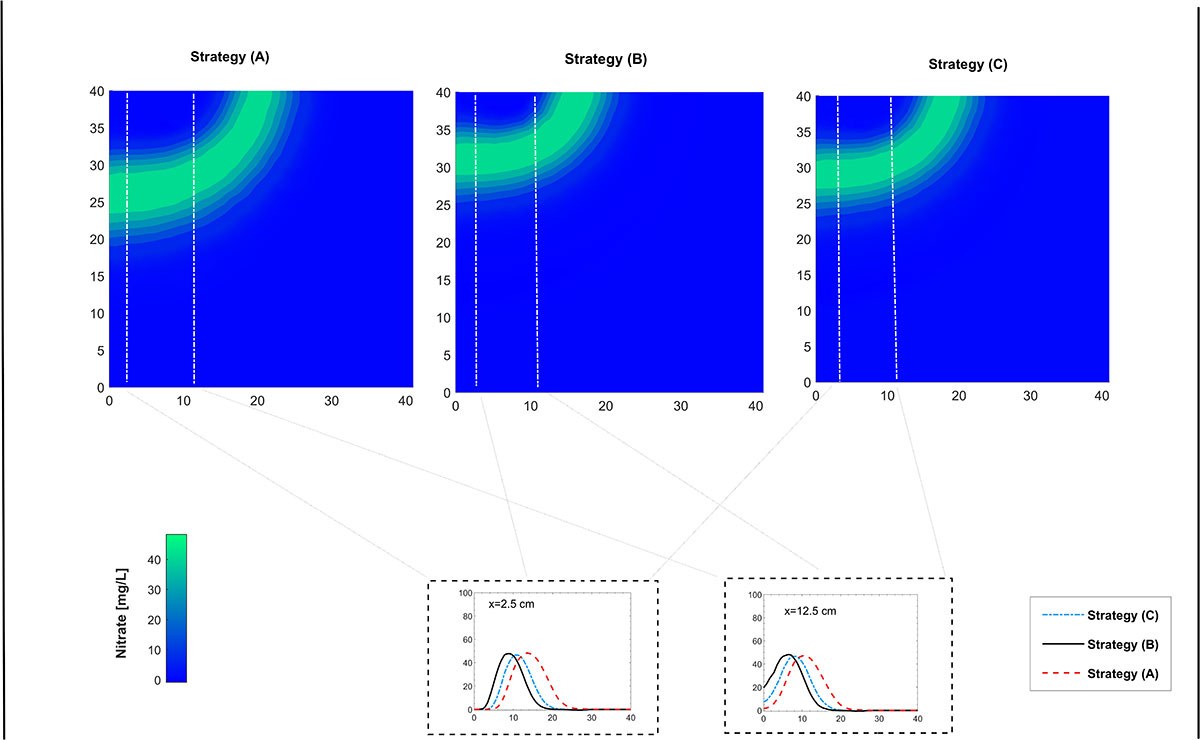
As shown in Figure 4, Strategy B demonstrates good performance by maintaining nutrient concentrations in the root zone for longer, which supports efficient plant uptake. In contrast, Strategies A and C lead to excessive nitrate leaching into deeper soil layers, reducing fertilizer efficiency and posing risks of groundwater contamination. Importantly, these outcomes were accurately captured with our proposed scheme, confirming its ability to reproduce complex fertigation scenarios while significantly reducing computational costs. This demonstrates how our approach can support the design of irrigation strategies that optimize both crop yield and environmental protection.
Figure 4: Nitrate distribution after 6 hours of fertigation for the three strategies using the proposed method (Toutlini et al. 2025a).
Beyond nitrate transport, our tests (in the paper) showed that the scheme performs well in other challenging cases:
- Infiltration through heterogeneous soils — maintaining stability under difficult conditions.
- Groundwater recharge — accurately reproducing groundwater rise and recharge dynamics under transient infiltration conditions.
- Soil salinity transport — reproducing reference results with reduced runtime.
Conclusion
Our research shows that advanced mathematical modeling can be made accessible and efficient through modern computational techniques. By accelerating simulations of water and nutrient transport in soils, we enable farmers, engineers and scientists to evaluate multiple irrigation and fertilization strategies before applying them in the field. This leads to more efficient fertilizer use, reduced environmental risks, and improved crop yields.
Building on this work, we have extended the framework to include multiple fertilizers such as urea, ammonium, nitrate, phosphorus, and potassium, together with root water and nutrient uptake processes (Toutlini et al., 2025b, c). These developments expand the model’s capacity to address the challenges of sustainable agriculture in diverse soil and climate conditions.
Reference
Toutlini, N.-E., Beljadid, A., & Soulaïmani, A. (2025a). A semi-implicit second-order temporal scheme for solving the pressure head-based form of Richards' and advection–dispersion equations. Computers and Mathematics with Applications, 187, 106–131. https://doi.org/10.1016/j.camwa.2025.03.011
Toutlini, N.-E., Beljadid, A., & Soulaïmani, A. (2025b). A semi-implicit finite element method for modeling fertilizer transport through soils with root water and nutrient uptake. Mathematics and Computers in Simulation. Under Review.
Toutlini, N.-E., Soulaïmani, A., & Beljadid, A. (2025c). JAX-WSPM: A GPU-accelerated parallel framework using the JAX library for modeling water flow and solute transport in unsaturated porous media using an implicit finite element method. Computer Physics Communications. In press.
Li, J., Zhang, J., & Rao, M. (2005). Modeling of water flow and nitrate transport under surface drip fertigation. Trans. ASAE, 48(2), 627-637.
