Vibration des turbines hydroélectriques au démarrage

Contrôler les niveaux de vibration dans les turbines

Un aspect essentiel de la gestion des turbines hydroélectriques est le contrôle des niveaux de vibrations. Tant dans la phase de conception que pendant l’exploitation, une bonne compréhension du comportement vibratoire est capitale pour prédire l’état de fissuration des turbines. Le phénomène le plus critique en vibration est la résonance. Lorsqu’une excitation coïncide avec un mode propre de la structure, les vibrations sont amplifiées, ce qui accélère la fissuration (voir Figure 1). Cette dégradation précoce se couple à un manque de précision des modèles numériques, qui ne parviennent pas à simuler parfaitement les effets de résonance dans les turbines.

Figure 1 : Turbine gravement fissurée. [1]

Cause principale des résonances : les démarrages-arrêts

À l’instar d’une vieille voiture qui vibre intensément au démarrage et à l’arrêt, les turbines subissent de fortes sollicitations pendant ces phases. Dans un cas comme dans l’autre, ces fortes vibrations sont dues à de multiples résonances. Au moment du démarrage-arrêt, la vitesse de rotation varie, ce qui permet aux vibrations de couvrir une large bande de fréquence, augmentant de ce fait la probabilité de générer une résonance.

Si les démarrages-arrêts de turbines étaient occasionnels il y a encore quelques années, ils sont aujourd’hui monnaie courante. En effet, le développement des énergies éoliennes et solaires génère de forts aléas de production, et une partie du parc hydroélectrique est utilisé pour stabiliser les fluctuations du réseau. En conséquence, l’exploitation continue des installations a laissé place à une exploitation intermittente, augmentant de ce fait les cycles de démarrage-arrêt des turbines jusqu’à un facteur 100. La figure 2 montre que le taux de dommages générés par ces cycles est particulièrement préoccupant.

Pour combler les lacunes de l’approche numérique, notre équipe s’est concentrée sur le développement d’une méthode expérimentale capable de caractériser les phénomènes de résonance.

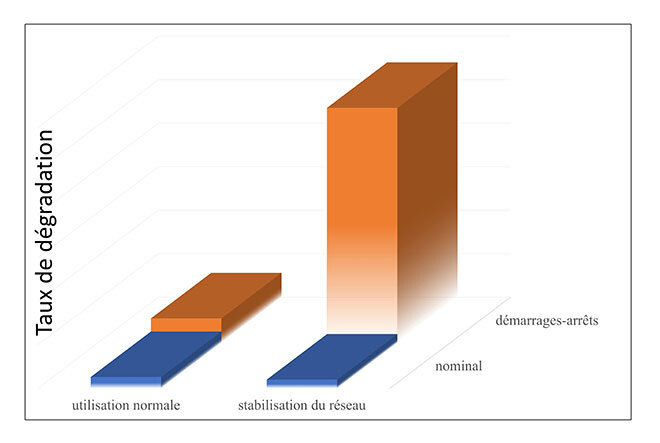
Figure 2 : L’utilisation des groupes pour stabiliser le réseau accroît drastiquement les dommages structuraux. Données issues de [1].

Caractérisation expérimentale des résonances

L’idée centrale de l’approche expérimentale est d’exploiter des mesures de vibration pour caractériser fidèlement le comportement des turbines. Mathématiquement parlant, les résonances sont modélisées à l’aide de deux paramètres : la fréquence et l’amortissement. Ces derniers sont appelés paramètres modaux. En théorie, de très nombreux algorithmes dans la branche de l’analyse modale opérationnelle sont capables d’estimer ces paramètres [2]. Seulement, ces modèles nécessitent des données de bonne qualité pour obtenir des résultats fiables. Typiquement, les données doivent être stationnaires et nombreuses pour obtenir un problème bien conditionné. Cela permet d’analyser de nombreuses résonances conjointement, et de moyenner les mesures pour « lisser » les observations. Dans le cadre de nos travaux, les mesures proviennent de régimes transitoires non-stationnaires. Le seul moyen de garantir la stationnarité des signaux est de considérer de courts intervalles de temps. En conséquence, les données sont très peu nombreuses, et il est nécessaire de traiter les résonances individuellement, sans possibilité de moyenner les données.

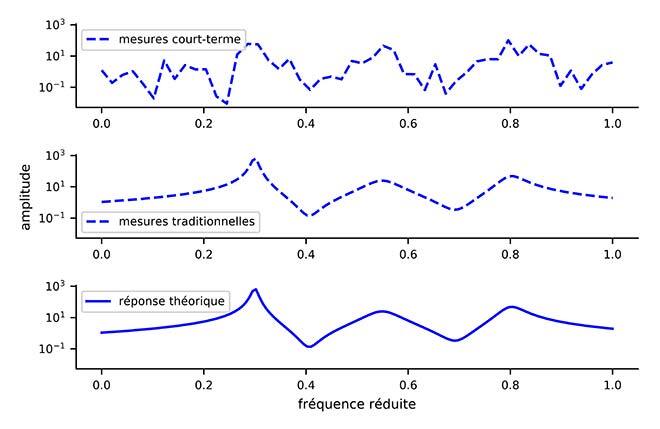
Figure 3 : Comparaison d’un modèle de résonance (3 résonances) selon des mesures de bonne qualité et de mauvaise qualité.

La Figure 3 montre la différence notable entre un problème bien conditionné et notre problème. La difficulté à traiter les données court terme est palpable. Le traitement des données doit donc répondre à deux défis : premièrement, séparer les différentes résonances mesurées simultanément pour pouvoir les traiter individuellement, et deuxièmement, mettre en place une procédure d’identification efficiente avec peu de données, capable d’estimer les incertitudes.

Analyse modale par suivi d’ordres synchrones

Pour répondre aux spécificités des données court terme, notre équipe a travaillé sur le développement d’un nouvel algorithme d’identification.

Le premier objectif est de trouver une approche qui permette de séparer les différentes résonances présentes simultanément dans les données. La solution trouvée repose sur un principe d’excitation sélective. Si la plupart des excitations rencontrées sur les turbines produisent des résonances avec n’importe quel mode, certaines excitations ont des propriétés sélectives. Ces dernières ne peuvent produire de résonances qu’avec certains modes précis. C’est typiquement le cas des harmoniques de la vitesse de rotation. Lors du démarrage ou de l’arrêt de la turbine, ces harmoniques couvrent une large bande de fréquence, et peuvent générer des résonances sélectives avec des modes particuliers. Sur la Figure 4, il est montré comment les harmoniques sont utilisées pour séparer les contributions, alors que tous les modes sont généralement excités en même temps. Il existe des algorithmes qui permettent d’extraire les résonances avec les harmoniques : les outils de suivi d’ordres synchrones [3]. Une fois mis en œuvre, ces outils isolent une résonance court terme qui doit être caractérisée.

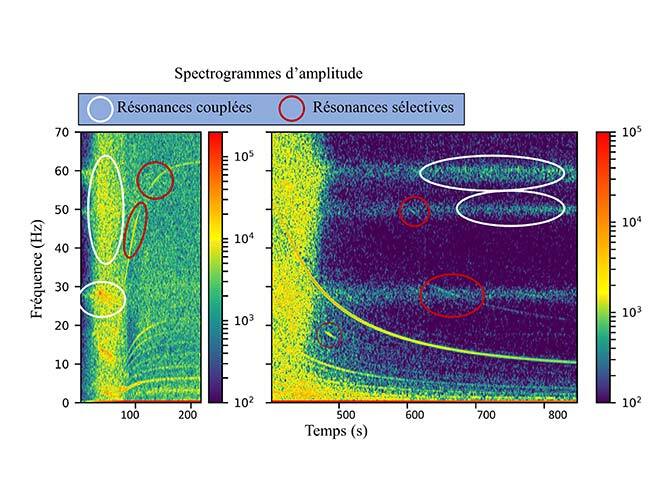
Figure 4 : analyse temps-fréquence de mesures de contrainte. Les résonances rencontrées lors de démarrages (gauche) et d’arrêts (droite) peuvent être séparées par les harmoniques de la vitesse de rotation.

La caractérisation de données court terme se prête bien à l’utilisation d’approches bayésiennes. Ces dernières permettent d’estimer les paramètres modaux avec peu d’échantillons et d’y associer des marges d’incertitudes fiables. En général, le principal défaut de ces approches est le temps de calcul requis pour atteindre une convergence. La procédure bayésienne rapide est capable de réaliser l’identification des paramètres modaux en maintenant des temps de calcul raisonnables [4]. La technique a été testée avec succès sur des exemples numériques. Une comparaison explicite avec les modèles classiques est proposée en Figure 5.

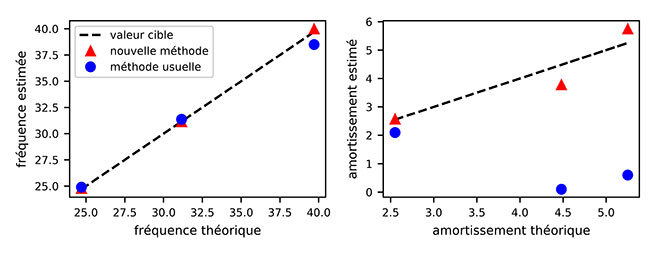
Figure 5 : comparaison des capacités d’identification des approches usuelles et de notre approche. La technique bayésienne rapide montre de meilleurs résultats pour l’amortissement.

Des résultats encourageants

La combinaison du suivi d’ordre et du solveur bayésien rapide a permis, pour la première fois, d’estimer les paramètres modaux réels d’une roue de turbine hydroélectrique dans un régime de démarrage-arrêt. Un exemple de la méthode est résumé à la Figure 6. Ces travaux préliminaires sont encourageants, mais des efforts accrus sont actuellement portés sur la réduction des marges d’incertitudes, encore élevées.

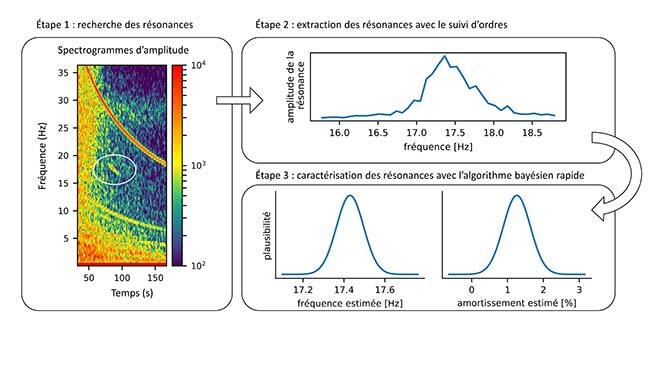
Figure 6 : synthèse de la méthode. L’analyse modale est couplée au suivi d’ordre pour réaliser une caractérisation fiable des résonances.

D’un point de vue industriel, ces résultats sont susceptibles d’apporter une amélioration significative des capacités de prédiction numérique dans des phases critiques d’exploitation. En effet, les paramètres identifiés expérimentalement peuvent être implantés dans des routines d’assimilation de données, permettant ainsi la calibration des approches numériques et garantissant des simulations plus représentatives de la réalité.

Pour aller plus loin…

Les lecteurs intéressés par ce sujet peuvent consulter l’article suivant :

Q. Dollon, J. Antoni, A. Tahan, M. Gagnon, C. Monette, Operational Modal Analysis of hydroelectric turbines using an order based likelihood approach, Renewable Energy 165-1, 2021. pp.799-811