18 March 2024
Execution-Time Reduction Mechanism for Flip Decoders of Polar Codes
Summary
Error detection and correction play a key role in modern communication systems, ensuring data integrity and reliability. Polar codes are a class of error-correcting codes. At the impractical requirement of infinite code length, these are proven to be theoretically optimal under low-complexity successive cancellation (SC) decoding. SC flip (SCF) decoding has been proposed to provide better error-correction performance compared to SC decoding at shorter code lengths. However, SCF comes at the cost of highly variable execution times. In this work, we propose a simplified restart mechanism (SRM) to reduce execution times of flip decoders while providing identical error-correction performance.
Keywords: decoding, error correction codes, polar codes, successive cancellation flip, memory management, execution time
Introduction
An error-correcting code allows a receiver to detect and, when used properly, correct most if not all errors in an information block corrupted during transit from the transmitter to the receiver. An encoder uses an (N,k) error-correcting code to transform k bits of information into a sequence of length N, effectively adding redundancy to a message before its transmission. The ultimate goal of error correction is to successfully decode k information bits with as little effort as possible.
Polar codes sparked the interest of researchers, being the first type of error-correction code proven to be asymptotically optimal under low-complexity decoding, SC [1]. However, when short-to-moderate code lengths are used, SC provides subpar error-correction capability. SC list (SCL) decoding improves decoding performance by using L parallel SC decoder instances. Despite the increased decoding complexity, the error-correction performance of SCL motivated the selection of polar codes to protect the control channel in the latest generation of mobile communication, i.e., 5G New Radio.
As an alternative to SCL decoding, SC flip (SCF) decoding was proposed, where a single instance of SC is reused over multiple decoding trials. SCF flips only one bit per trial. The maximum number of trials T_max is applied to limit latency and complexity. Overall, the SCF is less complex than SCL, but is not deterministic in its execution time. Next, DSCF-3 designates the dynamic SCF decoding algorithm [2] which can flip up to 3 bits per trial.
In this work, we propose a simplified restart mechanism (SRM) that reduces the average execution time of SCF decoding for polar codes, without affecting error-correction performance.
Description of the Simplified Restart Mechanism
Figure 1 Proposed SRM on a decoding tree for a (8.4) polar code flipping the û6 bit
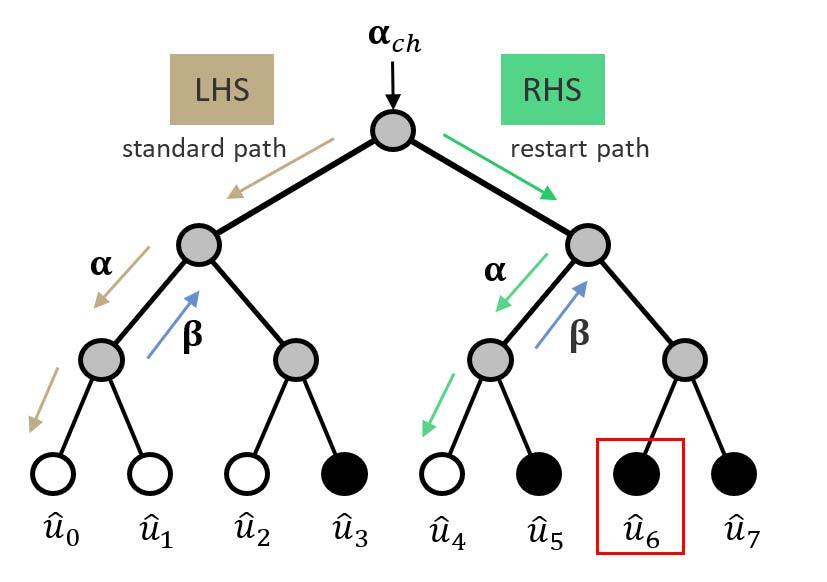
A (N,k) polar code is composed of k information bits and (N-k) frozen bits, i.e., bits known to both the encoder and the decoder, and set to 0.
Figure 1 presents the decoding tree for a (8,4) polar code. The information from the channel is αch={α0,…,α7} and enters through the tree root while bit estimates û={û0,…,û7} are generated at the tree leaves. The frozen bits are the white circles and have a value of 0. A bit decision on the bit estimate is made for each information bit represented in black circles. Hence, a wrong estimate (and a bit flip) can only happen in that location.
Under SCF, if the first trial fails, at least one decision bit is wrong. The decoder estimates the location to flip, performs another trial, flips the estimate once it reaches the location previously identified, then resumes decoding until the end.
The additional trial remains unchanged until facing the first bit estimate to flip. If the information bit is located on the right-hand side (RHS) of the decoding tree, the tree on the left-hand side (LHS) can be skipped. In Figure 1, the bit flip is f1=6>8/2, the (LHS) is skipped and the decoding restarts at the (RHS) decoding tree.
Thus, the proposed SRM allows skipping calculations in some additional trials of the decoder. The mechanism does not alter the error-correction performance but comes at the cost of small memory overhead.
Efficiency of the Proposed Mechanism
Analysis of the SRM is performed by simulating a transmission using a (1024, 128) polar code over the AWGN channel. The polar code is decoded either by SCF or DSCF-3 decoders with Tmax=12 and Tmax=301, respectively. We analyzed the error-correction performance and the average execution time. SC decoding characteristics were also provided for reference.
Figure 2 Error-correction performance of SCF and DSCF-3 decoders with and without our proposed SRM.
Figure 3 Average execution time of SCF and DSCF-3 decoders with and without our proposed SRM. Latency of SC decoding included for reference
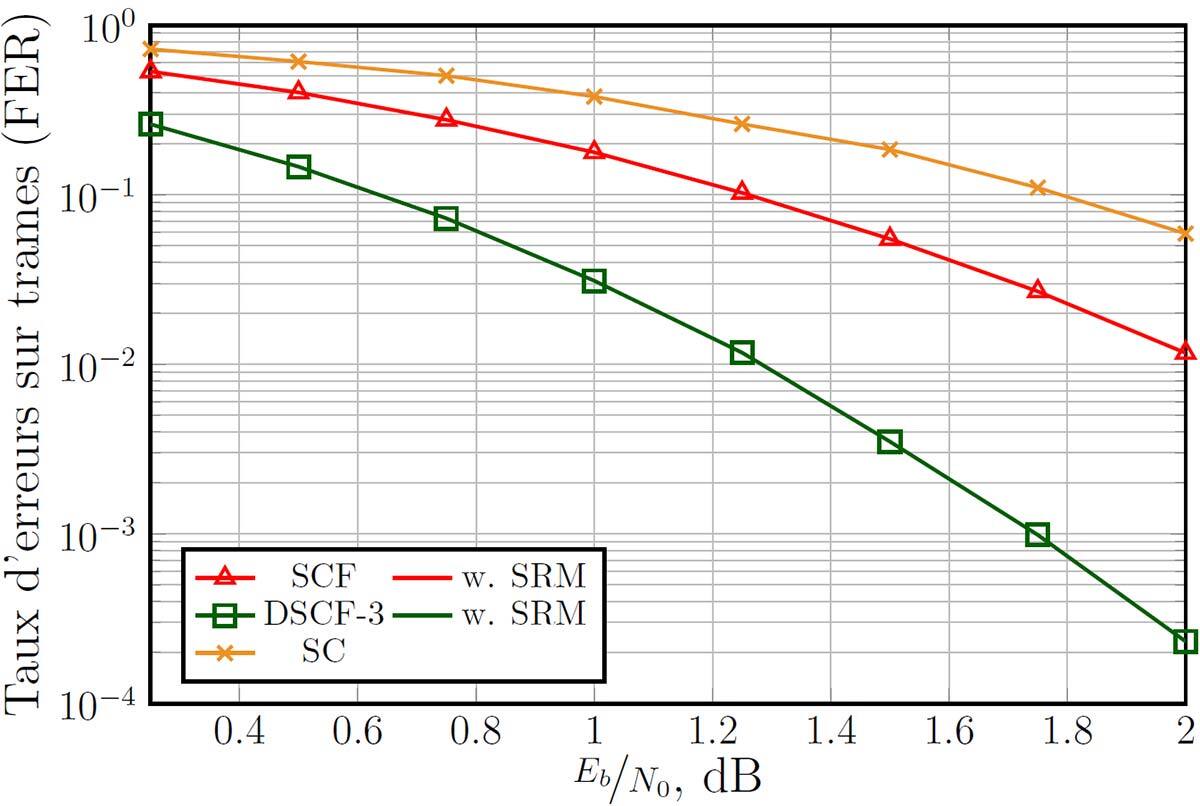
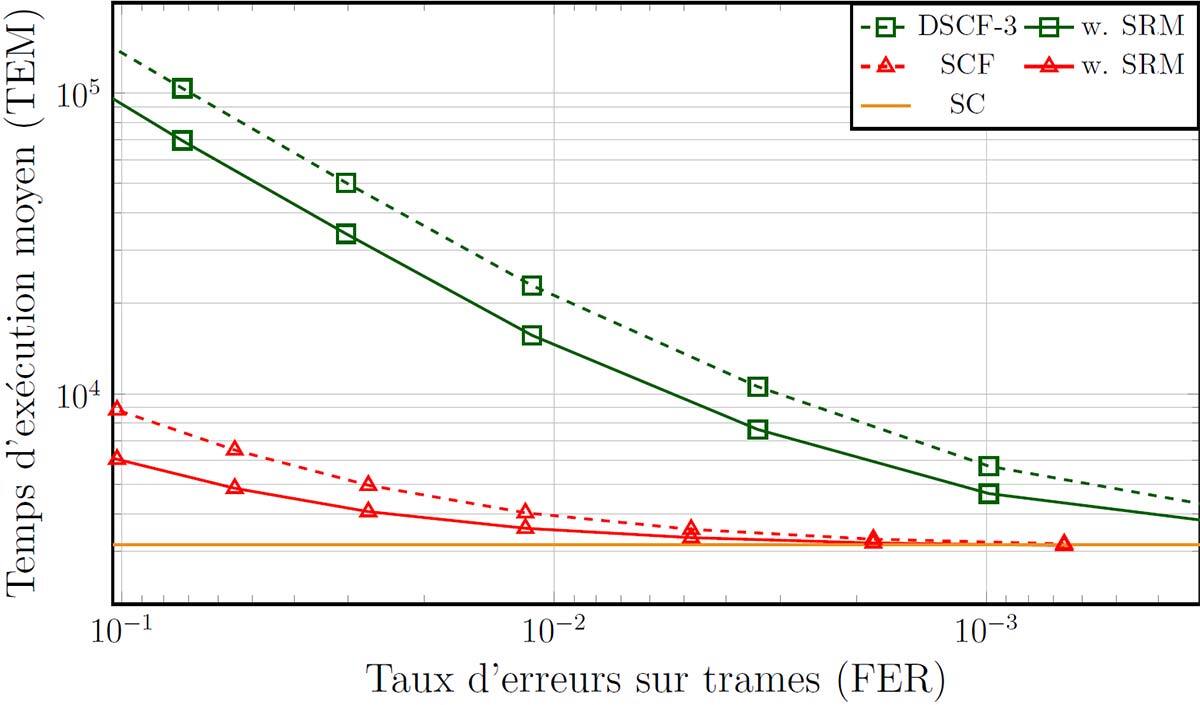
Figure 2 shows the error-correction performance in terms of frame-error rate (FER), i.e., the ratio of successfully decoded frames over the total number of frames. The x-axis is the Eb/N0, expressed in dB, which indicates the signal-to-noise ratio (SNR) per bit. For smaller Eb/N0, the noise energy in the channel is high compared to that of the signal, making it more difficult to decode a frame. Both flip decoders show improvements compared to the SC decoder. As expected, the FER decreases for both decoding methods, when the signal quality improves, and the SRM is confirmed not to affect the error-correction performance.
Figure 3 depicts the average execution time (AET), where the solid and dashed lines correspond to the flip decoders, with and without the SRM, respectively. The AET is expressed in number of clock cycles (CC) for computations in a realistic hardware implementation [3]. The x-axis is expressed in FER from Figure 2. SC decoding is provided as the bound. The decoders with SRM provide noticeable average execution-time reduction. The reduction is greater for the DSCF-3 decoder compared to SCF. For 1 wrongly decoded frame over 100, the AET reduction for DSCF-3 is 31.70%, compared to 11.17% for SCF.
Conclusion
Error-correction coding is a crucial part of communication; it allows us to detect and correct errors in the transmitted information. SC flip decoders for polar codes are of special interest for systems that are limited in hardware resources. However, the non-deterministic execution time of SC flip decoders makes those decoders more challenging to integrate in fixed-time systems. In this work, we proposed a mechanism to reduce the average execution time and complexity of SC flip decoders for polar codes while maintaining the same error-correction capability. Our results showed that the average execution time can be reduced by 31% with a standard flip decoder for polar codes.
References
[1] E. Arıkan, “Channel polarization: A method for constructing capacity-achieving binary-input memoryless channels”, IEEE Trans. Inf. Theory, vol. 55, no. 7, pp. 3051-3073, July 2009, doi: 10.1109/TIT.2009.2021379.
[2] L. Chandesris, V. Savin and D. Declercq, "Dynamic-SCFlip Decoding of Polar Codes," in IEEE Trans. Commun., vol. 66, no. 6, pp. 2333-2345, June 2018, doi: 10.1109/TCOMM.2018.2793887.
[3] C. Leroux, A. J. Raymond, G. Sarkis and W. J. Gross, "A Semi-Parallel Successive-Cancellation Decoder for Polar Codes," in IEEE Trans. Signal Process., vol. 61, no. 2, pp. 289-299, Jan.15, 2013, doi: 10.1109/TSP.2012.2223693.
For more information, please refer to our manuscript:
[4] I. Sagitov et al, “Successive-cancellation flip decoding of polar codes with a simplified restart mechanism,” IEEE Wireless Commun. And Netw. Conf. (WCNC), Glasgow, United Kingdom, 2023, pp. 1-6, doi: 10.1109/WCNC55385.2023.10119097.
