Simuler le monde plus rapidement

Image publiée avec la permission de CM Labs Simulations. Droits d’auteur.
L’une des applications inestimables de la technologie de réalité virtuelle (RV) est la formation d’utilisateurs à des tâches spécialisées qui sont coûteuses ou difficiles à réaliser dans un environnement réel comme, par exemple, former un chirurgien à effectuer une procédure délicate, ou un grutier à contrôler un équipement de construction. Ce dernier exemple est précisément le type de scénario visé par notre récent projet mené en collaboration avec l’entreprise montréalaise CM Labs Simulations. CM Labs conçoit des simulateurs de formation basés sur la physique pour les véhicules lourds, les équipements de construction et la robotique à l’aide de son simulateur propriétaire appelé Vortex. Ses simulations se doivent d’être performantes, stables et précises. Les solutions typiques conçues pour jeux vidéo et autres applications interactives ne peuvent satisfaire tous ces critères : des algorithmes spécialisés sont donc nécessaires.
Simuler la physique par petits composants
Au cours d’une collaboration précédente avec CM Labs (Peiret et al, 2019), nous avons mis au point une nouvelle technique pour paralléliser la simulation de systèmes mécaniques complexes d’après une approche de décomposition de domaine appelée méthode du complément de Schur. Cette approche décompose la simulation en sous-systèmes contigus et utilise efficacement les processeur multicœur présent dans la plupart des ordinateurs modernes. Elle a permis de multiplier par près de 14 la vitesse de calcul de certains scénarios de formation (voir le figure 1), et ce, sans sacrifier la précision de la simulation.

Figure 1 – La méthode du complément de Schur (en bas à gauche) permet de multiplier par près de 14, par rapport au solveur de base, la vitesse de simulation de ce scénario de formation sur des grues en tandem soulevant des objets.
Simulations sous forme de graphe
Bien que la technique de parallélisation proposée ait grandement contribué à améliorer les performances, celles-ci varient en fonction de la manière dont la simulation globale est décomposée en sous-systèmes. C’est ici que nos travaux les plus récents jouent un rôle important. Nous avons analysé le modèle du système mécanique sous forme de graphe, où les objets physiques sont les sommets du graphe, et les contraintes cinématiques qui couplent le mouvement d’objets (par exemple, les joints et contacts mécaniques) sont les arêtes.

Figure 2 – Graphe de différentes simulations : une chaîne tombant sur le sol (à gauche), un tas compact de cailloux (au centre) et une tour de rondins sur le point de s’effondrer (à droite).
Algorithmes de partitionnement de graphe
Le graphe objet-contrainte est la base sur laquelle repose la décomposition d’une simulation, ce qui mène à la question suivante : quelle est la meilleure façon de décomposer la simulation ? Notre récent article examine l’efficacité de plusieurs algorithmes de partitionnement de graphe adaptés aux applications en temps réel : les algorithmes doivent pouvoir créer des partitions (ou des sous-systèmes) en quelques millisecondes seulement. Nous avons constaté qu’un algorithme gourmand qui étend chaque sous-système en alternant la minimisation et la maximisation du degré des sommets ajoutés produit une décomposition qui améliore la performance par rapport aux techniques de référence.
Par contre, nos travaux antérieurs ont révélé qu’un couplage accru entre les sous-systèmes réduit les performances du solveur. Nous cherchons donc, une fois le partitionnement initial calculé, à raffiner le graphe pour réduire davantage les arêtes entre chaque sous-système.
Algorithmes de raffinement
L’étape de raffinement réduit les connexions entre les sous-systèmes au moyen d’algorithmes de raffinement de graphe, à savoir les algorithmes de Kernighan-Lin (KL) et de Fiduccia-Mattheyses (FM). Ces algorithmes ont été largement utilisés dans d’autres domaines comme la conception de circuits, mais, selon nous, il s’agit de la première fois qu’ils sont appliqués dans le contexte de la simulation physique. En bref, l’algorithme KL se concentre sur la recherche d’une paire d’objets dans deux sous-systèmes et les échange pour réduire le nombre total d’arêtes entre les sous-systèmes. L’algorithme FM, quant à lui, joue au « tennis » en trouvant un seul objet à déplacer d’une partition à une autre partition adjacente. Cependant, l’analyse de tous les objets et de toutes les contraintes de la simulation prend beaucoup de temps, surtout pour les simulations d’objets rigides complexes et de grande taille. Par conséquent, nous améliorons l’efficacité des algorithmes de raffinement en suivant les objets périphériques de chaque partition et en appliquant les algorithmes de raffinement uniquement aux objets situés à l’interface entre les partitions.
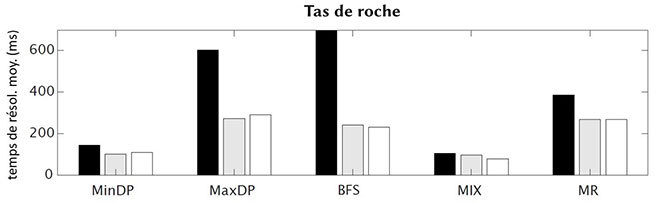
Figure 3 – Temps pour résoudre la dynamique de l’exemple du tas de cailloux. La stratégie de partitionnement que nous proposons (MIX) avec un raffinement KL (barre grise) ou FM (barre blanche) donne les meilleures performances.
Conclusion
La nouvelle méthode de partitionnement proposée est plus performante que les autres algorithmes que nous avons étudiés. En outre, le raffinement à l’aide des algorithmes KL et FM améliore encore plus les performances en réduisant le nombre d’arêtes du graphe entre les sous-systèmes. D’après nos expériences, nous avons vu que l’algorithme de partitionnement proposé peut améliorer les performances en diminuant jusqu’à 50 % le temps de calcul du solveur.
Information supplémentaire
Voyez les détails de cette recherche dans les articles suivants :
Peiret, A., Andrews, S., Kövecses, J., Kry, P. G. and Teichmann, M. (2019). “Schur Complement-based Substructuring of Stiff Multibody Systems with Contact”. ACM Transactions on Graphics (TOG), 38(5), 1-17.
Liu, Y. and Andrews, S. (2022). “Graph Partitioning Algorithms for Rigid Body Simulations”. Eurographics 2022 (Short Papers).



